格式：pdf
大小：79KB
頁數： 5頁
1 參數取值問題求解策略 一、參變分離 ,利用最值處理 若在等式或不等式中出現兩個變量，其中一個變量的范圍已知，另一個變量的范圍為所求，且容易 通過恒等變形將兩個變量分別置于等號或不等號的兩邊，則可將恒成立問題轉化成函數的最值問題求解。 例 1．已知當 x R時，不等式 a+cos2x<5 4sinx+ 恒成立，求實數 a的取值范圍。45a 分析：在不等式中含有兩個變量 a 及 x，其中 x 的范圍已知（ x R），另一變量 a 的范圍即為所求， 故可考慮將 a 及 x 分離。 解：原不等式即： 4sinx+cos2x< a+545a 要使上式恒成立，只需 a+5 大于 4sinx+cos2x 的最大值，故上述問題轉化成求 f(x)45a =4sinx+cos2x 的最值問題。 f(x)= 4sinx+cos2x= 2sin 2x+4sinx+1= 2(sinx 1) 2+3 3, ∴ a
格式：pdf
大小：42KB
頁數：
《風力發電科技發展"十二五"專項規劃》的出臺,是為了貫徹落實《國家中長期科學和技術發展規劃綱要(2006-2020年)》、《國民經濟和社會發展第十二個五年規劃綱要》、《國家戰略性新興產業發展規劃》、《國家"十二五"先進能源技術領域戰略》等國家相關可再生能源戰略部署,促進風能技術的發展和應用,為我國未來風電產業的可持續發展提供技術保障。《規劃》從現狀和形勢需求出發,明確了風力發電科技未來
熱門知識
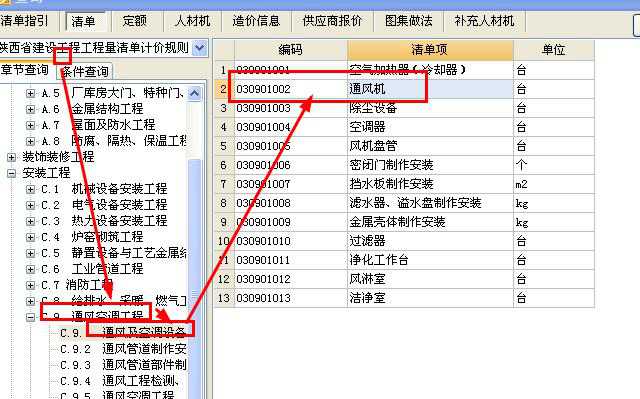
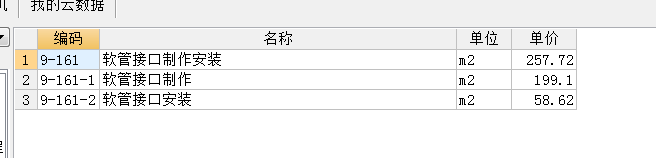
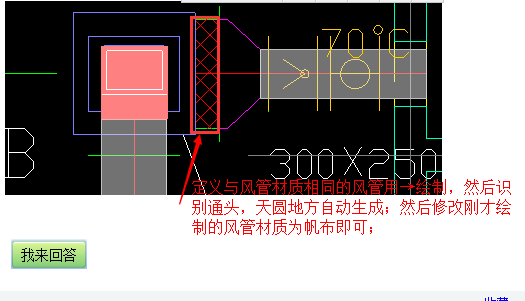
通風問題求-
話題： 工程造價yuanyuan89
-
話題： 工程造價tuolixoang
精華知識
通風問題求-
話題： 工程造價zhang_huahao
-
話題： 裝修工程liutao750316
最新知識
通風問題求-
話題： 工程造價wangyougen
相關問答
通風問題求
通風問題求相關專題
- 空氣調節與通風有什么區別
- 礦井通風具體是指哪幾點
- 礦井通風系統的介紹
- 礦井通風系統立體圖如何作
- 礦井通風的掘進通風
- 礦井通風系統有些什么設備
- 礦井通風系統包括哪些
- 離心式通風機的重量
- 糧庫通風地籠如何鋪設
- 置換通風以什么為動力
- 應用亞溫淬火工藝解決45鋼槽型螺母淬裂問題的探索
- 有關建筑工程造價管理面臨的問題與其處理手段
- 以BIM為基礎的裝配式建筑全生命周期管理問題
- 在建筑行業建立農民工工資保證金制度若干問題的思考
- 中國水環境污染治理社會化資金投入現狀、問題與對策
- 醫用潔凈空調系統設計調試中易忽視的問題及設計優化
- 園林景觀工程在推進城鄉宜居環境建設中的問題及思考
- 應用貴州省雨洪公式計算施工期設計洪水需注意的問題
- 在線解答合同、FIDIC、清單、工程管理問題實況
- 制定機械加工勞動定額切削用量時間標準若干問題
- 醫院手術部新風機組盤管冬季凍裂問題分析及防止方法
- 再談VRV空調系統設計與施工中有關問題的解決方法
- 智能建筑工程監理過程中的幾個問題及處理方法
- 引水隧洞TBM開挖施工質量控制及問題處理對策
- 有關公路工程BOT建設項目財務管理若干問題的思考
- 有關工程造價預結算審核存在問題及其解決對策
- 中低壓燃氣管道工程質量控制及常見問題處理教學提綱