久久精品动漫一区二区三区 ,三叶草gy8566,狠狠色丁香久久婷婷综合蜜芽五月

更新時間：2025.05.10

頭條 17個樹冰噴頭 4個蒲公英噴頭怎么配水泵 4個水泵

這就要看你是如何設計噴泉類型了，主要是要將同期噴水的連接在同一個泵體上，用程控開關分別控制水泵工作時間就可以了。

相關推薦

點到平面的距離(1)

格式：pdf

大小：168KB

頁數： 4頁

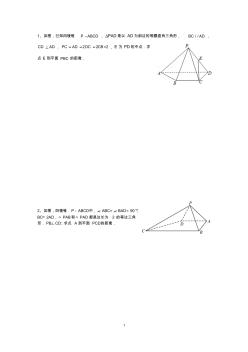
1 1、如圖，已知四棱錐 P ABCD ， PAD是以 AD為斜邊的等腰直角三角形， / /BC AD ， CD AD ， 2 2 =2PC AD DC CB ， E 為 PD的中點．求點 E 到平面 PBC 的距離 . 2、如圖，四棱錐 P－ABCD中，∠ ABC＝∠ BAD＝ 90°， BC＝ 2AD，△ PAB和△ PAD都是邊長為 2 的等邊三角形． PB⊥CD；求點 A到平面 PCD的距離． 2 3 、如圖，在四棱錐 P ABCD 中， / /C D P A D A BCD平面， 4 4, ,CD AD AB AC PA且 M 是線段 CP上一點 / / 1 1 = = 4 2 PM PC AP AD P DMB A平求面且，證， M ABCD并求點到平面的距離 4、如圖，四棱錐 P ABCD中，底面 ABCD 為平行四邊形， 60DAB

在線閱讀立即下載

點到平面的距離(文科)

格式：pdf

大小：223KB

頁數： 4頁

點到平面的距離 (文科數學 ) 1．【2018 年全國卷 II 文】如圖，在三棱錐中，，，為的中點．（1）證明：平面；（2）若點在棱上，且，求點到平面的距離．【答案】（1）見解析（ 2）．（2）作 CH⊥OM，垂足為 H．又由（ 1）可得 OP⊥CH，所以 CH⊥平面 POM．故 CH的長 F E D C BA 為點 C到平面 POM 的距離．由題設可知 OC= =2，CM = = ，∠ ACB=45°．所以 OM= ，CH= = ．所以點 C到平面 POM 的距離為．點睛：立體幾何解答題在高考中難度低于解析幾何，屬于易得分題，第一問多以線面的證明為主，解題的核心是能將問題轉化為線線關系的證明；本題第二問可以通過作出點到平面的距離線段求解，也可利用等體積法解決 . 2. （2005年福建高考題）如圖 1，直二面角 EABD 中，四邊形 A

在線閱讀立即下載

精華知識

樹冰噴頭與水面的距離

自動噴淋系統中，噴頭濺水盤距離燈具的距離應按多少來確定？ (2) 108

水平障礙物：噴頭濺水盤距常規燈具、送排風風口的平面距離不宜小于：0.3m.查看詳情

話題：地產家居
ldh123a
國家規范，消防自動滅火噴淋管網，噴頭與噴頭之間最大距離和最小距離各是多少。 (1) 69

詳見自動噴淋滅火系統設計規范我記得一般中危險級是最大距離3.6和最小距離2.4，離墻小于1.8 查看詳情

話題：工程造價
FEN^^
冰箱與煤氣灶的距離太近是怎么解決？ (1) 62

1、距離一般影響不大。不管是冰箱制冷，還是燃氣灶放熱，都影響不大。2、燃氣灶與冰箱太近，感覺有問題，更多是心理作用影響。3、如果感覺需要做些隔絕措施，建議將菜板放在冰箱與燃氣灶之間...查看詳情

話題：工程造價
夢想世界
冰箱與熱源的距離需要多遠？ (3) 94

您好，電冰箱不能放在暖氣附近，必須要遠離熱源，否則會影響冰箱的制冷效果。通常冰箱兩側預留10cm以上的空間即可，但如果附近有熱源，會影響冰箱的熱交換。如果附近有暖氣，至少要保持1米...查看詳情

話題：工程造價
舒海軍
冰箱與燃氣灶距離多少最合適？ (3) 99

燃氣灶一般距非防火材料200mm,即20公分。考慮到是冰箱，最好不要放在廚房，因為廚房油煙大，溫度高，而且冰箱本身也是要散熱的，對冰箱日常保養不利。 ??還有就是冰箱代表貯藏，聚財...查看詳情

話題：地產家居
lht20040101

分類檢索：

A
B
C
D
E
F
G
H
I
J
K
L
N
M
O
P
Q
R
S
T
U
V
W
X
Y
Z
0 - 9
符號

大肉大捧一进一出视频来了,肉嫁高柳1～4动漫在线观看,四虎影院176,波多野42部无码喷潮

樹冰噴頭與水面的距離

熱門知識

精華知識

最新知識

相關問答

分類檢索：